4.8 Random Walks & Pagerank

Consider the following random-walk graphs:

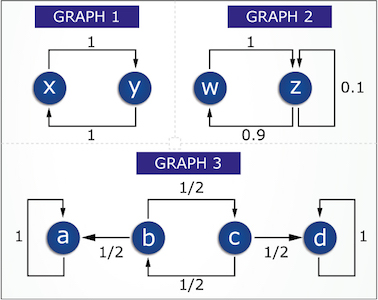
1. Find \(d(x)\) for a stationary distribution for graph 1.
   Exercise 1

    Numerical Response 

2. Find \(d(y)\) for a stationary distribution for graph 1.
   Exercise 2

    Numerical Response 

3. Find \(d(z)\) for a stationary distribution for graph 2. Please answer in a fraction of the form x/y.
   Exercise 3

    Numerical Response 

4. If you start at node \(x\) in graph 1 and take a (long) random walk, does the distribution over nodes ever get close to the stationary distribution?
   Exercise 4

    Yes 

    No 
   No, you will just alternate between nodes \(x\) and \(y\).
   CheckShow Answer