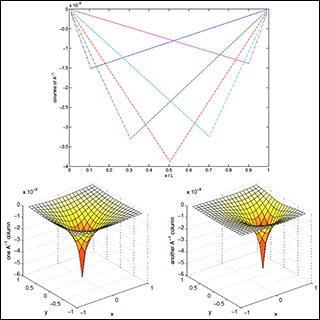
Colors of A-1 where A is a discretized ∇2 with Dirichlet boundary conditions. Top: several columns in 1d (Ω = [0,L] = [0,1]). Bottom: two columns in 2d (Ω = [1,-1] x [-1,1]. In both 1d and 2d, the location of minimum corresponds to the index of the column: this is the effect of the unit-vector "source" or "force" = 1 at that position (and = 0 elsewhere). (Image by Steven G. Johnson.)
Instructor(s)
Prof. Steven G. Johnson
MIT Course Number
18.303
As Taught In
Fall 2014
Level
Undergraduate
Course Description
Course Features
Course Description
This course provides students with the basic analytical and computational tools of linear partial differential equations (PDEs) for practical applications in science engineering, including heat / diffusion, wave, and Poisson equations. Analytics emphasize the viewpoint of linear algebra and the analogy with finite matrix problems. Numerics focus on finite-difference and finite-element techniques to reduce PDEs to matrix problems. The Julia Language (a free, open-source environment) is introduced and used in homework for simple examples.
Other Versions
Other OCW Versions
OCW has published multiple versions of this subject. ![]()
Archived versions: ![]()


